شرح مفهوم معامل الارتباط في الإحصاء وطريقة حسابه الصحيحة بدقة

شرح مفهوم معامل الارتباط في الإحصاء وطريقة حسابه الصحيحة بدقة، ففي حال أردنا تعريف الارتباط سنجد ببساطة أنه تحديد طبيعة وقوة للعلاقة بين متغيرين أو عدمها، وهذا يدل على أن هناك طريقة لمعرفة ذلك الارتباط، ألا وهو معامل الارتباط. الذي يمكن اعتباره مؤشرًا لذلك الارتباط في تحديد طبيعة العلاقة وقوتها وفق أشكال الارتباط الموجب السالب والمعتدل. حيث أن لكل منها شكل من أشكال الانتشار في العلاقة. نتيجةً لذلك إليكم عبر موقع تجارتي مقالًا سنتناول فيه تعريف معامل الارتباط في الإحصاء، وطريقة الحساب الصحيحة له. كما سنتعرف على أنواع معامل الارتباط في الإحصاء بالتفصيل مع أمثلة عن معادلات معامل الارتباط ليكون شرحنا سهلًا. فعلى الرغم من صعوبة ما قد تحمله تلك المعادلات والمعاملات، لكننا قد أوجزنا لكم كل ما يجب معرفته عن معامل الارتباط.

مفهوم معامل الارتباط في الإحصاء Correlation coefficient

المقصود بـ معامل الارتباط في الإحصاء هو مقياس رقمي إحصائي لقوة العلاقة الخطية بين متغيرين. ويرمز له بالرمز (R). حيث تتراوح قيمة معامل الارتباط من (-1) إلى (1) بين المتغيرين. حيث يصف المعامل الأول (-1) ارتباطًا سلبيًا أو عكسيًا مثاليًا. أما المعامل (1) هو الارتباط الإيجابي التام أو العلاقة المباشرة، بينما يشير المعامل 0 إلى عدم وجود علاقة خطية بين المتغيرين. على سبيل المثال، يتم استخدام معامل بيرسون الذي يقيس قوة واتجاه العلاقة الخطية بين متغيرين، ولكن يستطيع معامل بيرسون تقييم الارتباطات غير الخطية بين المتغيرات، كما لا يمكنه التفريق بين المتغيرات التابعة والمستقلة. وذلك لأنه يستخدم معادلة إحصائية رياضية لقياس مدى تقارب نقاط البيانات التي تجمع بين المتغيرين بالاعتماد على سلسة من قيم البيانات المرسومة على المحور (x) والقيم المقابلة للسلسلة الأخرى على المحور (y) لرصد تقارب الخط المناسب، علمًا أنه يتم تحديد الخط المناسب من خلال تحليل الانحدار. أما بالنسبة لمعاملات الارتباط المشتقة من أخذ العينات، فيعتمد تحديد الأهمية الإحصائية على القيمة (p) والتي يتم حسابها من حجم عينة البيانات بالإضافة إلى قيمة المعامل.

خصائص معامل الارتباط Correlation coefficient

يملك معامل الارتباط في الإحصاء عدة خصائص وهي كما يلي:

• يعتبر معامل الارتباط الإحصائي قيمة كمية تتراوح من (-1) إلى (1).
• إذا كانت نتيجة معامل الارتباط (0) فهذا يعني عدم وجود علاقة بين المتغيرين من البيانات.
• إذا كانت القيمة الخاصة بالمعامل (+1) أو (-1) فهذا يعني أن العلاقة بين المتغيرين مثالية.
• عندما يقترب المعامل من (-1) أو (+1) فهذا يعني أن الارتباط قوي.
• المتغيرات ستكون مرتبطة ارتباطًا مباشرًا في حال كان المعامل رقمًا موجبًا.

تفسير معامل الارتباط Correlation coefficient

هناك العديد من الإرشادات التي تفسر معامل الارتباط في الإحصاء، لأن النتائج يمكن أن تختلف بشكل كبير بحسب مجالات الدراسة. على الرغم من ذلك إن هذا التوجيه مفيد في جميع الأوقات وجميع مجالات الدراسة إلا أنه من المهم جدًا مراعاة سياق البحث، والغرض منه، عندما تريد الحصول على الاستنتاجات الصحيحة.

• من -1 إلى -7 سلبي قوي جدًا.
• من -5 إلى -7 سلبي قوي.
• من -3 إلى -5 سلبي معتدل .
• من 0 إلى – 3 سلبي ضعيف .
• 0 لا يوجد قيمة والمتغيرين متساويان.
• من 0 إلى 3 ضعيف إيجابي.
• من 3 إلى 5 معتدل إيجابي.
• من 5 إلى 7 قوي إيجابي.
• من 1 إلى 7 إيجابي قوي جدًا.

بشكل عام تتراوح قيمة معامل الارتباط في الإحصاء دائما بين (1) و (-1) ويجب التعامل مع هذه القيم على أنها مؤشر عام لقوة العلاقة بين المتغيرات. إذ تدل علامة المعامل على ما إذا كانت المتغيرات تتغير في نفس الاتجاه، أو في اتجاهين معاكسين. كما أن القيمة المطلقة للرقم تساوي الرقم بدون علامته، وتخبرك القيمة المطلقة لمعامل الارتباط بحجم ذلك الارتباط.

أنواع الارتباط

يوجد نوعين من الارتباط في تحليل معاملات الارتباط وهما:

• الارتباط الموجب الطردي: وهو علاقة بين متغيرين بحيث إذا تغير أحد المتغيرين فان الآخر يتبعه في نفس الاتجاه.
• الارتباط السالب: وهو علاقة بين متغيرين بحيث إذا تغير أحد المتغيرين فإن الآخر يتبعه في الاتجاه المضاد.

العلاقات الخطية في معامل الارتباط Correlation coefficient

يخبرك معامل الارتباط في الإحصاء بمدى ملاءمة بياناتك للخط، فإذا كانت لديك علاقة خطية فسيتم رسم خط مستقيم ويكون الحد لأفضل ملائمة. بحيث يأخذ في الاعتبار جميع نقاط البيانات الخاصة بك في مخطط التبعثر، وكلما اقتربت نقاطك من هذا الخط زادت القيمة المطلقة لمعامل الارتباط وزادت قوة الارتباط الخطي. أما في حال كانت جميع النقاط على ذلك الخط تماما فسيكون لديك ارتباط كامل. أما إذا كانت جميع نقاط البيانات قريبة من ذلك الخط فإن القيمة المطلقة لمعامل الارتباط الخاصة بك مرتفعة. في حال كانت تلك النقاط منتشرة بعيدًا عن الخط المستقيم، فإن القيمة المطلقة لمعامل الارتباط الخاص بك منخفضة. إن ميل الخط أو انحداره لا يرتبط بقيمة معامل الارتباط، إذ لا يساعدك معَامل الارتبَاط في التنبؤ بمدى تغير أحد المتغيرات بناءً على تغيير معين في الآخر. وذلك لأن مجموعتي البيانات لهما نفس قيمة معامل الارتباط، كما يمكن أن يكون لهما خطوط ذات ميول أو منحدر مختلف جدًا. اقرأ أيضًا: إدارة التسويق

كيف يتم تحليل الانحدار في معامل الارتباط Correlation coefficient

يتم تحليل الانحدار في معامل الارتباط في الإحصاء (بيرسون) عبر مراقبة زيادة المعَامل عن الصفر. فكلما زاد المعَامل عن الصفر كلما كان التوافق أفضل وزاد الارتباط سواء أكان ارتباطًا موجبًا أم سالبًا. حيث تصف القيم (-1 / 1) التقلبات المناسبة من خلال محاذاة جميع نقاط البيانات في خط مستقيم، مما يشير إلى أن المتغيرات مرتبطة تمامًا. بعبارة أخرى يمكن التنبؤ بالعلاقة بين المتغيرين عن طريق تحديد قيمة أحد المتغيرات ومقارنتها بالقيمة للمتغير الآخر. وكلما اقترب معَامل الارتبَاط من الصفر كلما كان الارتباط أضعف والعكس صحيح. أما في حال كان الارتباط صفرًا فهو يشير إلى أنه لا توجد أي علاقة خطية بين المتغيرين. علاوةً على ذلك، تختلف تقييمات قوة الارتباط على أساس قيمة معامل الارتباط باختلاف التطبيق. على سبيل المثال، في الفيزياء والكيمياء يجب أن يكون معامل الارتباط أقل من (-0.9) أو أعلى من (0.9) حتى يتم اعتبار علاقة الارتباط ذات مغزى. علمًا أنه يمكن أن تصل العلاقة إلى الحد الأدنى (-0.5)  أو أن يكون منخفضا مثل (0.5).

أهمية معامل الارتباط في الإحصاء Correlation coefficient

يتم استخدام معامل الارتباط في الإحصاء في العلوم والتمويل وذلك بهدف تقييم درجة الارتبَاط بين متغيرين أو عاملين أو مجموعة بيانات. على سبيل المثال، نظرًا لأن أسعار النفط المرتفعة مواتية لمنتجي النفط الخام، فيفترض أن العلاقة بين أسعار النفط والعوائد على مخزونات النفطية ستكون إيجابية جدًا. عن طريق حساب معامل الارتباط لهذه المتغيرات بناءً على بيانات السوق التي تكشف عن وجود ارتباط إيجابي أو سلبي على مدى فترات طويلة.

معامل الارتباط والاستثمار Correlation coefficient

إن معامل الارتباط في الإحصاء مفيد بشكل خاص في تقييم وإدارة مخاطر الاستثمار. على سبيل المثال، تشير نظرية المحفظة الحديثة إلى أن التنويع يمكن أن يقلل من تقلب عوائد المحفظة ويحد من المخاطر. كما يمكن أن يشير معامل الارتباط بين العوائد السابقة إلى ما إذا كانت إضافة الاستثمار إلى المحفظة سيؤدي إلى تحسين تنوعها أم لا. نتيجةً لذلك، تعد حسابات الارتبَاط أيضًا عنصرًا أساسيًا في استثمار العوامل وهي استراتيجية لإنشاء محفظة بالاستناد إلى العوامل المرتبطة بالعوائد الزائدة وفي الوقت نفسه يستخدم المتداولون الكمّيون الارتباطات السابقة ومعاملات الارتباط لتوقع التغيرات على المدى القريب في أسعار الأوراق المالية.

دلالة معامل الارتباط Correlation coefficient

يمكن الحصول على معامل الارتباط في الإحصاء عن طريق مقارنته بمعيار للعلاقة بين المتغيرات. وقد تم تصنيف القيم في معاملات الارتباط في (قوية ومعتدلة وضعيفة)، ويتم اعتماد أحدها في حال حصلت على نتيجة بين (-1 و 1). والتي تدل على وجود وقوة العلاقة بين المتغيرين وفيما إذا كانت إيجابية أم سلبية.

طريقة حساب معامل الارتباط بدقة Correlation coefficient

يمكن حساب معامل الارتباط في الإحصاء بطريقتين وهما:

• حساب معامل الارتباط عبر اكسل.
• حساب معامل الارتباط بالمعادلة.

حساب معامل الارتباط عبر إكسل excel

يمكن إيجاد معامل الارتباط في الإحصاء ضمن برنامج excel، وهي أبسط طريقة لحساب الارتباط عن طريق إدخال سلسلتين من البيانات في أعمدة متجاورة واستخدام صيغة الارتباط المضمنة. في حال كنت ترغب في إنشاء مصفوفة ارتباط عبر مجموعة من البيانات. فإن برنامج إكسل يحتوي على مكون إضافي لتحليل البيانات وذلك في تبويب (تحليل) ثم اختر (البيانات) ثم حدد جدول العوائد. وفي هذه الحالة يجب تسمية الأعمدة لديك، ليتعامل معها إكسل على أنها عناوين وذلك من خلال تحديد المربع (التسميات في الصف الأول). بعد ذلك يمكنك اختيار الإخراج على نفس الورقة في الصفحة، أو على ورقة جديدة. سيؤدي ضرب المدخلات إلى إنتاج مصفوفة الارتباط، ويمكنك إضافة بعض التنسيق النصي والشرطي للحصول على النتيجة .

حساب معامل الارتباط بالخطوات Correlation coefficient

إن عملية حساب معامل الارتباط في الإحصاء ليست صعبة فهي خطوات روتينية إلى حدٍ ما. لكن تجميع تلك الخطوات هو ما يصعب من العملية (وهي الورطة الحقيقية). حيث يعتبر حساب الانحراف المعياري بحد ذاته مملاً سيما وأن حساب معامل الارتباط لا يعتمد على الانحراف المعياري فقط! بل على العديد من العمليات الأُخرى. لذا إليكم طريقة حساب معامل الارتباط بالخطوات:

1. نبدأ ببعض العمليات الحسابات الأولية و سنستخدم المتبقي من تلك الحسابات في الخطوات اللاحقة.
   • احسب x̄ (متوسط جميع الإحداثيات الأولى للبيانات).
   • احسب ȳ (متسوط كل الإحداثيات الثانية للبيانات).
   • احسب s x (الانحراف المعياري للعينة لجميع الإحداثيات الأولى للبيانات  xi).
   • احسب s y  الانحراف المعياري للعينة لجميع الإحداثيات الثانية للبيانات yi).
2. استخدم الصيغة  (z_x)_i = (x_i – x̄) / s _x  واحسب القيمة المعيارية لكل xi.
3. استخدم الصيغة (z_y)_i = (y_i – ȳ) / s _y واحسب القيم m المعيارية لكل yi.
4. اضرب القيم المعيارية المقابلة (z_x)_i(z_y)_{i .} 
5. أضف البيانات إلى ناتج الضرب بعضهم.
6. قسّم المجموع من الخطوة السابقة على (n – 1) حيث (n) هو العدد الإجمالي للنقاط في مجموعة البيانات المقترنة.
7. نتيجة القسمة من الخطوة السابقة هو معامل الارتباط (r).

مثال تطبيقي على حساب معامل الارتباط بالخطوات

لنرى كيف يتم الحصول على معامل الارتباط (r) بدقة:

• نبدأ بقائمة البيانات المزدوجة وهي (1 , 1) (2 , 3) (4 , 5) (5 , 7).
• متوسط قيمة (x) ، متوسط  1 و 2 و 3 و 4 و 5 هو x̄ = 3.
• لدينا أيضًا ȳ = 4.

إن الانحراف المعياري لقيم x هو: (sx = 1.83) و (sy = 2.58) على الشكل التالي: يلخص الجدول أعلاه الحسابات اللازمة لحساب معامل الارتباط. إن المجموع في العمود (z_xz_y) هو 2.969848. نظرًا لوجود إجمالي أربع نقاط ولأن (4-1 = 3). نقسّم مجموع حاصل الضرب على (3) وهذا يعطينا معامل ارتباط (r = 2.969848/3 = 0.989949.).

أنواع معاملات الارتباط Correlation coefficient

يتم استخدام أنواع مختلفة من معاملات الارتباط لتقييم الارتباط بناءً على خصائص البيانات التي تتم مقارنتها. ويمكنك الاختيار بين العديد من أنواع معاملات الارتباط المختلفة بناءً على العلاقة الخطية، ومستوى قياس المتغيرات، وتوزيع البيانات الخاصة بك. نتيجةً لذلك إذا أردت الحصول على نتيجة إحصائية قوية ودقيقة من الأفضل استخدام معَامل الارتبَاط الأكثر ملاءمة لبياناتك من الأنواع التالية:

• معامل بيرسون:
  • معامل خطي.
  • متغيرين كميين (فاصل أو نسبة).
  • توزيع طبيعي.
• معامل رو سبيرمان:
  • معامل غير خطي.
  • متغيرين ترتيبيين أو متغيرين فاصلين.
  • توزيع متعدد.
• Point-biserial:
  • معامل خطي.
  • متغير ثنائي ومتغير كمي واحد (فاصل زمني أو نسبة).
  • توزيع طبيعي.
• Cramér’s V (Cramér’s φ):
  • معامل غير خطي.
  • متغيرين غير اسميين.
  • توزيع متعدد.
• Kendall’s tau:
  • معامل غير خطي.
  • متغيرين ترتيبيين أو متغيرين فاصلين.
  • توزيع متعدد.

معامل بيرسون Pearson coefficient

هو المعامل الأكثر شيوعًا وذلك لأنه يسمح بالحصول على استدلالات قوية ومعلميه تقيس العلاقات الخطية. لكن في حال كانت بياناتك لا تفي بجميع الافتراضات الخاصة بهذا المعامل، فستحتاج إلى استخدام اختبار غير معلمي بدلًا من ذلك. حيث تلخص الاختبارات غير المعلمية في معاملات الارتباط، ارتباط الرتب والعلاقات غير الخطية بين المتغيرات ويمكنك استخدام كل من (Spearman’s rho) و (Kendall’s tau) اللذان يتمتعان بنفس شروط الاستخدام. علمًا أنه يفضل استخدام (Kendall’s tau) للعينات الصغيرة، واستخدام (Spearman’s rho) للعينات الكبيرة.

افتراضات معامل بيرسون Pearson coefficient

أما الافتراضات التي يجب تتواجد في بياناتك فهي:

• يجب أن يكون كلا المتغيرين على مستوى الفاصل الزمني أو نسبة القياس.
• يجب أن تتبع البيانات من كلا المتغيرين للتوزيعات العادية.
• يجب ألا تحتوي بياناتك على قيم متطرفة.
• يجب أن تكون البيانات الخاصة بك من عينة عشوائية أو تمثيلية.
• يجب أن تتوقع علاقة خطية بين المتغيرين.

إن اختبار بيرسون هو اختبار حدودي، لذا فهو يتمتع بقدرة عالية على قياس العلاقة، لكنه ليس مقياسًا جيدًا إذا كانت المتغيرات الخاصة بك لها علاقة غير خطية، أو إذا كانت بياناتك تحتوي على قيم متطرفة، أو توزيعات منحرفة، أو تأتي من تغيرات فئوية. وفي حال لم تستوفي بياناتك أي من تلك الافتراضات فيجب استخدام معامل ارتباط الرتبة.

حدود معامل ارتباط بيرسون Pearson coefficient

يُقال أن الارتباط لا يقتضي السببية، و لا يمكن لمعامل بيرسون تحديد ما إذا كان أحد المتغيرات المرتبطة يعتمد على الآخر. كما لا يظهر معامل بيرسون نسبة التباين في المتغير التابع الذي يُنسب إلى المتغير المستقل. وهذا يظهر من خلال معَامل التحديد المعروض باسم (R-squared) الذي يمثل ببساطة معَامل الارتبَاط التربيعي. بالإضافة إلى ذلك، لا يصف معَامل الارتبَاط ميل الخط الأنسب. بل يمكن تحديد الميل باستخدام المربعات الصغرى في تحليل الانحدار. كما لا يمكن استخدام معَامل الارتبَاط بيرسون لتقييم الارتباطات غير الخطية أو الناتجة عن عينات البيانات التي لا تخضع للتوزيع الطبيعي. بل يمكن تحديدها من خلال القيم المتطرفة (نقاط بيانات بعيدة عن مخطط الانتشار الخاص بالتوزيع)، ويمكن تحليل تلك العلاقة باستخدام طرق غير بارامترية أو غير معلمية. على سبيل المثال، معَامل ارتبَاط سبيرمان، أو معَامل ارتبَاط رتبة كيندال، أو معَامل الارتبَاط متعدد الألوان.

صيغة معامل بيرسون Pearson coefficient

على الرغم من أن معامل ارتباط بيرسون معقد جدًا، إلا أن معظم برامج الكمبيوتر يمكنها أن تفرز معامل الارتباط من بياناتك بسرعة. ويتم ذلك ببساطة عبر تقسيم الصيغة للتباين المشترك بين المتغيرات على حاصل ضرب الانحرافات المعيارية. عند استخدام معادلة معامل الارتباط في الإحصاء (بيرسون) فستحتاج إلى التفكير فيما إذا كنت تتعامل مع بيانات من عينة أو من المجتمع بأكمله. حيث تختلف صيغ العينة والسكان في رموزها ومدخلاتها، ويطلق على معامل ارتباط العينة اسم (r) بينما يسمى معامل الارتباط السكاني (rho) وهو الحرف اليوناني (ρ). ويستخدم معامل ارتباط العينة تباين العينة بين المتغيرات، وعينة الانحرافات المعيارية وفق المعادلة التالية: بينما يستخدم معامل الارتباط في الإحصاء السكاني التباين السكاني بين المتغيرات، والانحرافات المعيارية للسكان وفق المعادلة التالية:

مثال تطبيقي على معامل الارتباط بيرسون Pearson coefficient

لحساب ارتباط عبر المعامل بيرسون يجب البدء بتحديد الانحراف المعياري لكل متغير، بالإضافة إلى التباين بينهما. وذلك لأن معامل الارتباط هو التغاير مقسومًا على حاصل ضرب الانحرافات المعيارية للمتغيرين.

(​ρxy​= Cov(x,y) ÷ σx​ ​σy​)

• ρxy​: معامل الارتباط اللحظي الناتج من معامل بيرسون.
• Cov(x,y): هو التغاير بين المتغيرين x/y.
• σx: هو الانحراف المعياري ل x.
• σy: هو الانحراف المعياري ل y.

إن الانحراف المعياري هو مقياس تشتت البيانات من متوسطها، كما يُظهر التباين ما إذا كان المتغيرين يميلان إلى التحرك في نفس الاتجاه. بينما يقيس معامل الارتباط قوة تلك العلاقة على مقياس معياري من (-0) إلى (0).

معادلة تطبيق معامل بيرسون Pearson coefficient

يتم استخدام معامل الارتباط في الإحصاء (بيرسون) بعد الحصول على عينة من البيانات وتطبيق المعادلة التالية:

 n×(∑(X,Y)−(∑(X)×∑(Y))) ـــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــــ        = r (n×∑(X2)−∑(X)2)×(n×∑(Y2)−∑(Y)2) ​√

• r: هو معامل الارتباط.
• n: هو عدد الملاحظات.

معامل الارتباط Spearman’s rho

يعتبر معامل الارتباط في الإحصاء الترتيبي (Spearman’s rho) هو البديل الأكثر شيوعًا لبيرسون، كونه يستخدم تصنيفات البيانات من كل متغير. على سبيل المثال، (من الحد الأدنى إلى الأعلى) بدلًا من البيانات الأولية نفسها، لذلك يتم استخدام (Spearman’s rho) عندما تفشل البيانات في تلبية افتراضات معامل بيرسون. ويحدث هذا عندما تكون أحد المتغيرات على مستوى قياس ترتيبي، أو عندما لا تتبع البيانات من أحد المتغيرين أو كليهما التوزيعات الطبيعية. بينما يقيس معامل ارتباط بيرسون العلاقة الخطية بين البيانات. يقيس (Spearman’s rho) معَامل ارتبَاط رتابة العلاقات. وفي العلاقات الخطية يتغير كل متغير في اتجاه واحد بنفس المعدل عبر نطاق البيانات في علاقة ترتيبية. بحيث يتغير المتغير دائمًا في اتجاه واحد فقط، ولكن ليس بالضرورة بنفس المعدل! فالعلاقات الرتبية هي أقل تقييدًا من العلاقات الخطية وتكون كما يلي:

• رتابة موجبة: عندما يزيد أحد المتغيرات ويزيد الآخر أيضًا.
• رتابة سالبة: عندما يزيد أحد المتغيرات ويقل المتغير الآخر.

معادلة معامل ارتباط الرتبة لمعامل سبيرمان Spearman’s rho

إن رموز (Spearman’s rho) هي (ρ) لـ معامل الارتباط في الإحصاء السكاني، و (rs) لمعَامل العينة، (بينما تحسب الصيغة معَامل ارتبَاط بيرسون بين تصنيفات البيانات المتغير). ومن أجل استخدام صيغة (Spearman’s rho) يجب أن تقوم أولًا بترتيب البيانات من كل متغير بشكل منفصل من الأدنى إلى الأعلى. بحيث تحصل كل نقطة بيانات على ترتيب من الأول أو الثاني أو الثالث الخ. وبعد ذلك ستجد الفروق (di) بين تصنيفات المتغيرات الخاصة بك لكل زوج من البيانات التي يجب اعتبارها المدخل الرئيسي للصيغة وهي:

• di: هو الفرق بين رتبة المتغير (x) ورتبة المتغير (y) لكل زوج من البيانات.
• ∑d2i: هو مجموع تربيع الفروق بين متغير (x) و  (y).
• n: هو حجم العينة.

إذا كان لديك معامل ارتباط بقيمة (1) فإن جميع التصنيفات لكل متغير تتطابق مع كل زوج من البيانات. وإذا كان لديك معامل ارتباط (-1) فإن تصنيفات أحد المتغيرات هي عكس ترتيب المتغير الآخر تمامًا. أما معامل الارتباط القريب من الصفر يعني أنه لا توجد علاقة رتيبة بين التصنيفات المتغيرة.

مثال تطبيقي على معامل الارتباط Spearman’s rho

في البداية يجب أن نرتب البيانات قبل البدء في حساب معامل الارتباط في الإحصاء (رتبة سبيرمان). علمًا أنه في حال زيادة متغير واحد فإن المتغير الآخر سيتبع علاقة رتيبة. أما الآن إليكم خطوات الحصول على معامل الارتباط سبيرمان:

1. يجب إنشاء جدولًا للبيانات التي حصلت عليها.
2. رتب مجموعتيّ البيانات، ويمكن ترتيبها من خلال تخصيص الترتيب من 1 (الأكثر قيمة) و 2 (الأقل) إلخ… وبعدها ستحصل على أصغر قيمة على الترتيب الأدنى، ويجب أن يتم ذلك على مجموعتي القياس.
3. أضف عمود ثالث (d) إلى مجموعة البيانات الخاصة بك لتشير إلى الرتب. على سبيل المثال، إذا كان ترتيب الفيزياء للطالب الأول هو 3، وترتيب الرياضيات 5. فإن الاختلاف هو 3 في العمود الرابع  بعد تربيع قيم العمود (d).

   فيزياء	مرتبة	كيمياء	مرتبة	د	مربع د
   35	3	30	5	2	4
   23	5	33	3	2	4
   47	1	45	2	1	1
   17	6	23	6	0	0
   10	7	8	8	1	1
   43	2	49	1	1	1
   9	8	12	7	1	1
   6	9	4	9	0	0
   28	4	31	4	0	0
   					12

4.  اجمع كل قيم مربع (d) وهي 12 (∑d square).

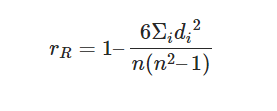
الحل باستخدام معامل الارتباط سبيرمان

نعوض تلك القيم بتطبيق معامل سبيرمان على البيانات أعلاه نستنتج:

• = 1 – ( 6 × 12 ) / ( 9 (81-1) ).
• = 1-72 * 720.
• = 1-01.
• = 0.9، وهو ارتباط مثالي.

معامل ارتباط فاي Phi coefficient

يسمى أحيانًا بمتوسط معامل الارتباط في الإحصاء الطوارئ للمربع، وهو مقياس للارتباط بين متغيرين ثنائيين، كما يستخدم لقياس جودة التصنيفات الثنائية من (mcc) وهو مشابه لمعامل بيرسون. حيث يتم اعتبار العلاقة بين متغيرين إيجابية في حال كانت معظم البيانات تقع على طول الخطوط القطرية، بينما تكون العلاقة سلبية عندما تكون معظم البيانات ليست قطرية.

تفسير معامل فاي Phi coefficient

على غرار معامل الارتباط في الإحصاء (بيرسون) يأخذ معامل فاي القيم بين (-1) و (1) حيث تكون كما يلي:

• -1: يشير إلى علاقة سلبية بين المتغيرين.
• 0: يشير إلى عدم وجود علاقة بين المتغيرين.
• 1: يشير إلى وجود علاقة إيجابية تمامًا بين متغيرين.

قد تصل النتيجة إلى (+ 70) أو أعلى لتكون علاقة إيجابية قوية جدًا، بالمقابل قد تصل إلى (- 70) وتكون علاقة سلبية قوية جدًا. وتتدرج العلاقة ( قوية جدًا – قوية – معتدلة – ضعيفة – لا علاقة) بحسب نتيجة معامل الارتباط. بشكل عام كلما كان معامل فاي بعيدًا عن الصفر، كانت العلاقة بين المتغيرين أقوى وكان هناك دليل أكثر على نوع من النمط المنهجي بين متغيرين.

مثال تطبيقي على معامل ارتباط فاي Phi coefficient

يتم حساب معامل الارتباط في الإحصاء (فاي) في حال كان لدينا البيانات التالية: يمكن حساب معامل فاي كما يلي: Φ = (AD-BC) / √ (A + B) (C + D) (A + C) (B + D)

معامل الارتباط الخطي الجزئي partial linear correlation coefficient

يقيس معامل الارتباط في الإحصاء (الإرتباط الجزئي) قوة العلاقة بين متغيرين مع التحكم في تأثير واحد أو أكثر من المتغيرات الأخرى. على سبيل المثال، قد ترغب في معرفة ما إذا كان هناك ارتباط بين كمية الطعام التي يتم تناولها وضغط الدم، مع التحكم في الوزن و مقدار التمارين الرياضية. من الممكن التحكم في متغيرات متعددة تسمى متغيرات التحكم، أو المتغيرات المشتركة. ولكن مع ذلك لا ينصح عادةً بأكثر من واحد أو اثنين من المتغيرات، لأنه كلما زادت متغيرات التحكم قلت موثوقية نتائج الاختبار.

مثال تطبيقي على معامل ارتباط جزئي partial linear correlation coefficient

إن الارتباط الجزئي له متغير مستقل مستمر (X) ومتغير تابع واحد مستمر (Y)، وهذا هو نفسه كما في تحليل الارتباط العادي في مثال ضغط الدم أعلاه. إن المتغير المستقل هو كمية الطعام المتناولة، والمتغير التابع هو ضغط الدم، ويجب أن تكون متغيرات التحكم وهي الوزن ومقدار التمرين مستمرة أيضًا.

• مدخول السعرات الحرارية (X ₁ ).
• مقابل ضغط الدم (X ₂ ).
• أثناء التحكم في الوزن (X ₃ ).

بالتعويض في معادلة معامل الارتباط الجزئي (r_12.3) يستخدم معَامل الارتبَاط (R) لإظهار نتائج الارتباط الجزئي مثل معَامل الارتبَاط العادي وتُرجع المعادلة (r_partial)  قيمة تتراوح من (-1) إلى (1). عادةً ما يتم تنفيذ الارتباط الجزئي عن طريق إجراء تحليل الانحدار المتعدد، الذي يتضمن بعض البرامج المرتبطة جزئيًا.

تفسير معامل الارتباط الجزئي partial linear correlation coefficient

إذا كان الارتباط الجزئي (r_12.3) أصغر من الارتباط البسيط لمتغيرين (R12)، ولكنه أكبر من (0) فإن المتغير (3) يفسر جزئيًا الارتباط بين (X) و(Y).

معادلة معامل الارتباط الجزئي partial linear correlation coefficient

إليكم فيما يلي معادلة معامل الارتباط في الإحصاء الجزئي:

أما معادلة الشكل العام للارتباط الجزئي من الانحدار المتعدد فهو كما يلي:

معامل الارتباط شبه الجزئي Semi-partial correlation coefficient

معامل الارتباط في الإحصاء شبه الجزئي هو نفس الارتباط الجزئي تقريبًا وفي الواقع يستخدم العديد من الأشخاص المصطلحين ليعنيان نفس الشيء. ومع ذلك يقوم الآخرون بالتمييز الدقيق وفق ما يلي:

• في الارتباط شبه الجزئي يظل المتغير الثالث ثابتًا بالنسبة لـ (X) و (Y) ولكن ليس لكليهما.
• في الارتباط الجزئي المتغير الثالث ثابت لكل من (X) و (Y).

على سبيل المثال، يمكن أن تخبرنا إحصائية الارتباط شبه الجزئي بالجزء المعين من التباين الذي يفسره متغير مستقل معين. ويشرح كيف يؤثر متغير مستقل واحد على المتغير التابع، بينما يتم التحكم في المتغيرات الأخرى، لمنعها من إعاقة عملية استخراج العلاقة.

مثال تطبيقي على المعامل شبه الجزئي Semi-partial correlation coefficient

لنفترض أننا حصلنا على مجموعة من البيانات من ورقة بحثية تسرد ثلاثة متغيرات على ستة أطفال. وتم اختبار كل طفل بقوة الذاكرة (Y)، ومعدل الكلام (X2) كما تم اتخاذ العمر بعين الاعتبار. والمطلوب إحصاء الارتباط الذي يتنبأ (Y) (قوة الذاكرة) من العمر (X1) و معدل الكلام (X2) . في الحالة التي يكون فيها (X1) و (X2) متغيرين عشوائيين مستقلين، سنكتشف مدى أهمية كل متغير عن طريق حساب معامل الارتباط التربيعي بين (X1) و (X2) والمتغير التابع (Y). كما سنعلم أن هذه المعَاملات التربيعية للارتبَاط كانت مساوية لمعَامل الارتبَاط المتعدد المربع. ولكن في المثال أعلاه فإن (X1) و (X2) ليسوا مستقلين، حيث يعتمد معدل الكلام على العمر بشكل كبير. وبالتالي فإن استخدام المعامل التربيعي سيحسب دور ومساهمة كل متغير عدة مرات.

معامل بوينت بايسيريال Point Bicerial Laboratories

هو معامل الارتباط في الإحصاء يستخدم يقيس علاقة الارتباط بين متغير كمي (X) ومتغير اسم (Y) ذي مستويين. مثل الإجابة بـ (نعم أو لا) أو الجنس (ذكر أو أنثى) وما إلى ذلك. ويشار إلى معَامل الارتبَاط بوينت بايسيريال إلى  (r_pb ). كما يُستخدم معَامل الارتبَاط بوينت بايسيريال لإيجاد درجة العلاقة بين متغيرين. الأول مجموعة الناجحين، والثاني مجموعة الراسبين أي متكافئون في النجاح والرسوب ويتم ذلك عبر ما يلي:

• نقسم المتغير (X) لمتغيرين كميين حسب مستويات:
• المستوى الأول (Y)  ويكون (Y₁) للنجاح، أو للإجابة بـ نعم.
• المستوى الثاني (Y₀) للرسوب أو للإجابة بـ لا .
• Y₁: يمثل المتوسط تحت المستوى الأول للمجموعة التي حصلت على الواحد.
• Y₀: يمثل المتوسط تحت المستوى الثاني للمجموعة التي حصلت على الصفر.
• S_Y: يمثل الانحراف المعياري للمتغير (Y).
• n: عدد المشاهدات الكلي .
• n₁: عدد مشاهدات المستوى الأول.
• n₀: عدد مشاهدات المستوى الأول.

هنا يكون السؤال، أوجد الارتباط بين الدرجة الكلية في اختبار اختيار من متعدد (Y) ودرجة إحدى فقرات الاختيار (X) لمجموعة مكونة من 10 طلاب بحسب الجدول التالي.

الحل باستخدام معامل بوينت بايسيريال Point Bicerial Laboratories

يتم الحل من خلال معامل بوينت بايسيريال Point Bicerial Laboratories وفق ما يلي:

• نحسب متوسط الدرجات الكلية للمجموعة الحاصلة على الواحد: Y^\₁ = i(1 + 3 + 5 + 5 + 6) ÷ 5 = 20 ÷ 5 = 4.
• كما نحسب متوسط الدرجات الكلية للمجموعة الحاصلة على الصفر: Y^\₀ =i(4 + 4 + 4 + 6 + 7) ÷ 5 = 25 ÷ 5 = 5.
• نحسب متوسط الدرجات الكلية Y^\ = i(1 +: 3 + 4 + 5 + 5 + 4 + 4 + 6 + 6 + 7) ÷ 10 = 45 ÷ 10 = 4.5.
• نحسب الانحراف المعياري بإكمال الجدول التالي ومنه تطبيق المعادلة: iS_Y² = Σ(Y-   )   ) Y^\)² ÷ n i أي  S_Y² = 26.5 ÷ 10 = 2.65 ومنها نأخذ الجذر التربيعي أي أن: S_Y = 1.63.

تطبيق معادلة معامل بوينت بايسيريال Point Bicerial Laboratories 

عبر تطبيق معامل بوينت بايسيريال Point Bicerial Laboratories وفق البيانات الواردة أعلاه نستنتج ما يلي:

معامل التحديد The coefficient of determination

عندما تقوم بتربيع معامل الارتباط في الإحصاء ستحصل على علاقة التحديد (r2)، وهي نسبة التباين المشترك بين المتغيرات. يكون معامل التحديد دائما بين (0) و (1) ويتم التعبير عنه غالبا كنسبة مئوية. كما يتم استخدام معامل التحديد في نماذج الانحدار لقياس مقدار التباين في أحد المتغيرات التي يتم تفسيرها من خلال تباين المتغير الآخر. كما يساعد في العثور على معادل الخط الأفضل ملاءمة ويمكن من خلال معامل التحديد التنبؤ بقيمة متغير واحد مع مراعاة قيم المتغير الآخر. بالإضافة إلى ذلك، تدل قيمة معامل التحديد (r2) المرتفعة إلى أن قدرًا كبيرًا من التباين في متغير واحد يتم تحديده من خلال علاقته بالمتغير الآخر. بينما تعني قيمة معامل التحديد (r2) المنخفضة أن جزءًا صغيرًا فقط من متغير واحد يمكن تفسيره من خلال علاقته بالمتغير الآخر. ويمكن أن يتم أخذ التباين في الحسبان من قبل العلاقات مع المتغيرات الأُخرى. غالبًا ما يبالغ معَامل الارتبَاط في تقدير العلاقة بين المتغيرات، وخاصةً العينات الصغيرة. لذلك يكون معامل التحديد مؤشرا أفضل للعلاقة. اقرأ أيضًا: الإحصاء Statistics 

معامل الاغتراب Alienation coefficient

يتم الحصول على معامل الارتباط في الإحصاء (الاغتراب) (1 – r²⁾ عندما يتم إزالة معَامل التحديد من الوحدة (1)، عن طريق طرح معَامل تحديد من (1). وهي نسبة التباين المشترك الذي لا يتم تقاسمه بين المتغيرات، أو هو التباين غير المبرر بين المتغيرات. يشير معَامل الاغتراب المرتفع إلى أن المتغيرين يشتركان في القليل من التباين المشترك. بينما يعني معَامل الاغتراب المنخفض إلى كمية كبيرة من التباين توجد في العلاقة بين المتغيرين.

طريقة اختيار معامل الارتباط المناسب correlation coefficient

تختلف معاملات الارتباط في الإحصاء باختلاف استخداماتها بناءً على نوع البيانات أو المتغيرات المراد إيجاد العلاقة بينها. حيث يمكن تحديد معَامل الارتبَاط المناسب عن طريق دراسة طبيعة البيانات المرصودة والمتغيرات لتحديد معَامل الارتبَاط المناسب.

استخدامات معامل الارتباط correlation coefficient

يتيح معامل الارتباط في الإحصاء إمكانية قياس قوة العلاقة بين كافة الظواهر أو البيانات المختلفة متمثلةً بمتغيرين مختلفين. ويتم تحديد الترابط بين المتغيرات مع المتغيرات الأخرى، مما يوضح مدى وقوة العلاقة بينهما وفيما إذا كانت العلاقة موجودة أم لا.

الفرق بين الارتباط والانحدار

إن الفرق بين معامل الارتباط في الإحصاء والانحدار هو أن لكل منهما تحليل قائم على التوزيع الخاص بالمتغيرات. وفيما يلي سنتعرف على تعريف الارتباط وتعريف الانحدار للتمكن من التفريق بينهما:

تعريف معامل الانحدار

إن الانحدار هو طريقة إحصائية ويتم استخدامه من خلال الرسم البياني بين متغيرين. حيث يعمل المستخدم على جمع العديد من متغيرات البيانات للحصول على العلاقة بينها. ولا يمكن الحصول على العلاقة بين المتغيرين إلا باستخدام معَامل الانحدار.

تعريف معامل الارتباط

إن الارتباط هو مقياس يوضح مدى وقوة العلاقة بين المتغيرات. ويتم استخدام المعامل الخاص بالارتبَاط بناءً على نوعية البيانات المرصود لقياس مدى التوافق والتغييرات التي تحدث في متغير واحد، بناءً على التغيرات التي تحدث على المتغير الآخر. نستنتج أن الفرق بين الانحدار والارتباط هو فيما يلي:

• يتيح الانحدار إمكانية تحديد شكل العلاقة بين متغيرين عشوائيين. بينما يوضح لك مُعامل الارتبَاط درجة تلك العلاقة وقوتها.
• يتيح لك الانحدار إمكانية المساعدة للحصول على النتائج الخاصة بالبحث والتنبؤ بها. بينما يساعدك المعامل على توفير المعلومات بما يتعلق بالبحث الذي تقيمه.

اقرأ أيضًا:تعريف التجارة

بماذا يستخدم معامل الارتباط في حياتنا correlation coefficient

لا شك في أنه تقابلنا في حياتنا العملية الكثير من المواقف التي تحتوي على ظاهرتين (متغيرين) وأكثر. ويكون المطلوب معرفة ما إذا كان هناك علاقة بين هذه المتغيرات، وما هو شكل العلاقة الموجودة بينها؟ وأيضًا كيفية التنبؤ بأحد هذين المتغيرين عندما نعرف المتغير الآخر. وهنا سنجد هذه الحالة في بعض المجالات التي تتضمن معدل الطول مع الوزن. حيث نستطيع أن ندخل الوزن لنحصل على الطول المناسب من خلال معادلة خاصة. تم التوصل إليها من خلال دراسة العلاقة بين المتغيرين (الطول والوزن) على مجموعة من الأفراد (البيانات).

الأسئلة الشائعة ؟